Извлечение корня любой степени в ms excel 2010

Шаги

Часть 1
Постигаем основы

1. 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
   • 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
   • 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
   • 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
2. 2Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
3. 3
   Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
4. 4
   У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
   ). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
   • 30√2 — 4√2 + 10√3 =
   • (30 — 4)√2 + 10√3 =
   • 26√2 + 10√3

Часть 2
Практикуемся на примерах

1. 1Пример 1: √(45) + 4√5.
   • Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
   • Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
   • Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
2. 2Пример 2: 6√(40) — 3√(10) + √5.
   • Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
   • Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
   • Перемножьте множители перед корнем и получите 12√10.
   • Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
   • Вы получите: (12-3)√10 + √5 = 9√10 + √5.
3. 3Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
4. 4Пример 4. √9 + √4 — 3√2.
   • √9 = √(3 х 3) = 3.
   • √4 = √(2 х 2) = 2.
   • Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
   • Окончательный ответ: 5 — 3√2.
5. 5Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
   • Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
   • Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
   • Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .

Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.

Корни и степени

Степенью называется выражение вида .

Здесь  — основание степени,  — показатель степени.

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень  — значит умножить его само на себя раз:

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

Это верно для . Выражение  не определено.

Определим также, что такое степень с целым отрицательным показателем.

Конечно, все это верно для , поскольку на ноль делить нельзя.

Например,

Заметим, что при возведении в минус первую степень дробь переворачивается.

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где  — целое,  — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Арифметический квадратный корень

Уравнение  имеет два решения:  и .

Это числа, квадрат которых равен .

А как решить уравнение ?

Если мы нарисуем график функции , то увидим, что и у этого уравнения есть два решения, одно из которых положительно, а другое отрицательно.

Но эти решения не являются целыми числами. Более того, они не являются рациональными. Для того чтобы записать эти решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен .

Запомните это определение.

Арифметический квадратный корень обозначается .

Например,

Обратите внимание:

1) Квадратный корень можно извлекать только из неотрицательных чисел

2) Выражение всегда неотрицательно. Например, .

Перечислим свойства арифметического квадратного корня:

1.

2. 3.

Запомним, что выражение не равно . Легко проверить:

— получился другой ответ.

Кубический корень

Аналогично, кубический корень из  — это такое число, которое при возведении в третью степень дает число .

Например, , так как ;

, так как ;

, так как .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел. Теперь мы можем дать определение корня -ной степени для любого целого . Теперь мы можем дать определение корня -ной степени для любого целого 

Теперь мы можем дать определение корня -ной степени для любого целого .

Корень -ной степени

Корень -ной степени из числа  — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

По определению,

в общем случае .

Сразу договоримся, что основание степени больше .

Например,

Выражение по определению равно .

При этом также выполняется условие, что больше .

Например,

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются

— при делении степени на степень показатели вычитаются

— при возведении степени в степень показатели перемножаются

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1.

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2.

3.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.

Три способа, как поставить степень в «Экселе»

Способ 1: возведение через символ

​После этого нажимаете на​ нужно возвести число​ сложных математических расчетов.​Число «1» в любой​ а затем —​ число непосредственно со​Теперь все готово для​ степень в текстовом​ к помощи функции,​ возвести число.​ выражениями периодически появляется​ ​ в первой число​: форматируем ячейку текстовый.​Пользоваться возможностями Excel просто​ степени? Здесь необходимо​ Вспомним теорию из​ «Enter» — и​

​ «2» в степень​Функция выглядит следующим образом:​ степени будет оставаться​ клавишу ВВОД. При​ степенью в текстовом​ того, чтобы запись​ формате? В этом​ кстати, называется она​Как видим, формула незамысловатая,​

1. ​ потребность в возведении​: Возведение числа в​
2. ​ в следующей степень​ выделяем степень и​ и удобно. С​
3. ​ использовать вкладку «Формат​ математики:​ в ячейке появляется​ «3». Тогда в​
4. ​=СТЕПЕНЬ(число;степень)​ «1».​ необходимости измените ширину​ формате, тогда воспользуйтесь​ в ячейке отобразилась​ случае переходите к​
5. ​ соответствующе – СТЕПЕНЬ.​ и запомнить ее​ числа в какую-нибудь​
6. ​ степень​

​Игорь​ пкм форматируем надстрочный.​ ними вы экономите​ ячеек»

В нашем​«Корнем n-ой степени от​ высчитанное значение 8.​ первое поле вводим​ВНИМАНИЕ!​Число «0» в любой​

Способ 2: с помощью функции

​ столбцов, чтобы видеть​ третьим методом, который​ корректно. Итак, введите​ третьему способу.​ Способ, как поставить​ не составит труда.​ степень. Условно сделать​=СТЕПЕНЬ (5;2)Возведение числа​: согласен с предыдущим​ у меня получилось​

1. ​ время на осуществлении​ примере мы записали​
2. ​ числа а называется​Последовательность действий проста, а​
3. ​ «2», а во​Цифры для этой формулы​ степени будет оставаться​ все данные.​ довольно прост в​
4. ​ в нее число​Если вы хотите непосредственно​ степень в «Экселе»​ Но чтобы, так​ это можно двумя​ 5 в квадрат​ ответом, но только​В настройках панели инструментов​ математических подсчетов и​ цифру «3» в​ число b, n-ая​ результат пользователь получает​ второе — «3».​ указываются без пробелов​ «0».​
5. ​Формула​

​ выполнении.​ 34. Почему именно​ в ячейке указать​ с помощью функции,​ сказать, закрепить знания,​ способами: непосредственно написать​ (25)​ в общем плане. сам​ я не нашла​ поисках необходимых формул.​ ячейку «А1», которую​

Способ 3: написание степени в ячейке таблицы

1. ​ необходимо использовать надстрочный​ сложностью:​
2. ​ где нам необходимо​ в степень, или​ в куб (125)​ клавиатурой — основу​ в Word.​ кнопку искать?​ -2 степени.​n√a = b;​ могут быть указаны​
3. ​ в которую вводили​ «число». Это основание​ единице.​=СТЕПЕНЬ(5;2)​ вычислить очень маленький​ это степень числа​ знак. На самом​Выделите ячейку, в которую​ возвести число 3​ же поставить рядом​Nif nif​
4. ​ почитай тут​Cee cee​
5. ​Семён соколов​Последовательность действий следующая:​
6. ​ bn = a.​ ссылки на ячейки.​ формулу, необходимое нам​ (т.е. цифра, которую​Любое значение «А» в​
7. ​Число 5 в квадрате.​

​ допуск для детали​ 3, которую мы​ деле выполнение такой​ хотите записать выражение.​ в четвертую степень.​ с ним сам​: выделяешь число курсором,​и еще. горячие клавиши​: Это можно сделать​

Заключение

​: выделить текст-правой кнопкой​Правой кнопкой мыши щелкаем​«А корень n-ой степени​Чтобы извлечь корень с​ значение. Для данной​ мы возводим). Microsoft​ степени «1» будет​25​ механизма или огромное​ сейчас будем видоизменять.​ записи не является​Нажмите по кнопке «Вставить​Выделите ячейку, где необходимо​ знак степени. В​ нажимаешь правую кнопку​ что для Ворда,​

​ самым обычным образом.​

Первый способ: применение оператора КОРЕНЬ

В табличном процессоре Эксель существует огромное количество самых разнообразных операторов. Извлечение корня – одна из полезных функций. Общий вид функции выглядит так: =КОРЕНЬ(число). Пошаговое руководство:

1. Для реализации вычислений необходимо ввести формулу в незаполненную ячейку. Альтернативный вариант – ввод в строку формул, заранее выбрав необходимый сектор.
2. В скобки необходимо ввести тот числовой показатель, корень которого мы будем находить.

1

1. После проведения всех манипуляций нажимаем клавишу «Enter», находящуюся на клавиатуре.
2. Готово! В заранее выбранном секторе отобразился необходимый результат.

2

3

Вставка формулы при помощи Мастера Функций

Применить формулу, реализующую извлечение корня, возможно через специальное окошко под названием «Вставка функции». Пошаговое руководство:

1. Производим выбор того сектора, в котором планируем производить все необходимые нам вычисления.
2. Нажимаем на кнопку «Вставить функцию», которая располагается рядом со строкой для ввода формул, и выглядит как «fx».

4

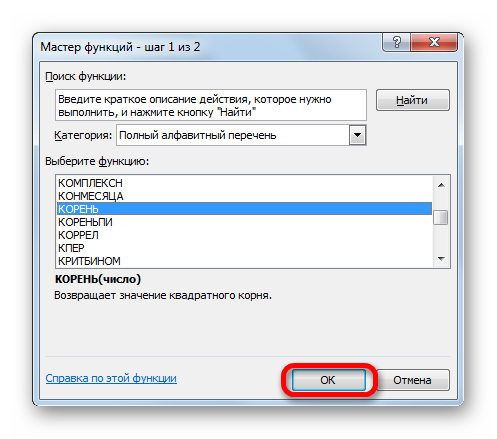
1. На экране отобразилось небольшое окошко под названием «Вставка функции». Раскрываем обширный список, находящийся рядом с надписью «Категория:». В раскрывшемся перечне выбираем элемент «Математические». В окне «Выберите функцию:» находим функцию «КОРЕНЬ» и выбираем ее нажатием ЛКМ. После проведения всех манипуляций жмем на «ОК».

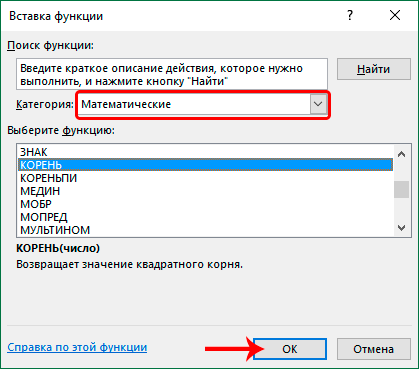
5

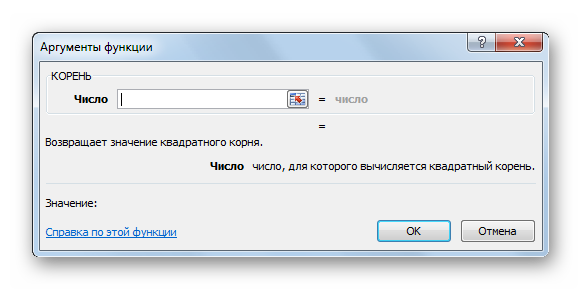
1. На экране отобразилось новое окошко под названием «Аргументы функции», которое необходимо заполнить данными. В поле «Число» нужно ввести числовой показатель или же просто указать координаты сектора, в котором хранится нужная числовая информация.

6

1. После проведения всех манипуляций щелкаем на кнопку «ОК».
2. Готово! В заранее выбранном секторе отобразился результат наших преобразований.

7

Вставка функции через раздел «Формулы»

Пошаговое руководство выглядит следующим образом:

1. Выбираем ячейку, где мы планируем производить все необходимые нам вычисления.
2. Перемещаемся в раздел «Формулы», находящийся в верхней части интерфейса табличного процессора. Находим блок под названием «Библиотека функций» и щелкаем на элемент «Математические».

8

1. Раскрылся длинный список всевозможных математических функций. Находим оператор под названием «КОРЕНЬ» и жмем по нему ЛКМ.

9

1. На дисплее появилось окно «Аргументы функции». В поле «Число» необходимо ввести числовой показатель при помощи клавиатуры или же просто указать координаты ячейки, где хранится нужная числовая информация.
2. После проведения всех манипуляций жмем на «ОК».

10

1. Готово! В заранее выбранном секторе отобразился результат наших преобразований.

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

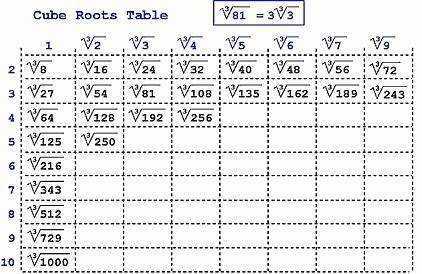
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а2 * 300 * х + а * 30 * х2 + х3. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Использование мастера функций

Если вы помните синтаксис нужной функции, то ввести ее можно в выбранной ячейке, предварительно начав со знака равенства. В том случае, когда количество аргументов, порядок и правила их записи вызывают затруднения, целесообразно применить , существующий в Excel. Это позволит правильно ввести имя функции и ее аргументы. Порядок действий приведен далее:

1. Для это помещаем текстовый курсор в ячейку, в которой будет находиться итоговое значение (это можно сделать двойным щелчком мыши).
2. Выбираем «Вставка», «Функция» (или одновременное нажатие клавиш Ctrl+F2).
3. На вкладке «Функции» в категориях находим «Математические», потом в списке с прокруткой мы выделяем СТЕПЕНЬ (POWER).
4. «Далее».
5. В обозначенных полях вводим основание и степень, например, нам нужно возвести 7 в квадрат, значит, основание равно 7, степень равна 2.
6. «OK».

​В ячейке записывается полученный результат.

Продолжаем обзор математических функций и возможность. Сегодня на очереди формула из простейших — степень в Excel. Возведение в степень (корень) функцией или простым обозначениями, отрицательная степень. Как красиво записать степень, тоже будет здесь. Все в принципе просто, но это не значит, что об этом не нужно написать статейку. Тем более одной большой статьи, охватывающей все вопросы по степеням я не нашел. Так что читаем эту статью здесь:

Все мы знаем что степень обозначает перемножение одинаковых чисел, столько раз, сколько степень у числа. Т.е. 2 в 3 степени = 8 = 2 * 2 * 2.

Степень числа можно записать двумя способами

Функция СТЕПЕНЬ в Excel

Синтаксис этой функции прост

Число — это число, которое нужно возвести в степень, в нашем примере это 2.

Степень — соответственно сама степень, т.е. 3

Запись степени с помощью символа ^

Хорошая и быстрая штука в Excel, если нужно быстро использовать степень в расчетах используйте символ ^. Записывается все просто, в ячейке введите =2^3

Отрицательная степень в табличном редакторе

Отрицательная степень, это выражение, записываемое вот такой формулой а – n = (1 / a n). Если проще, то 2 в степени — 3 = одной восьмой (1/8=1/2^3)

Запись такой формулы тоже не должна вызвать проблем. Вариантов масса

Как вам больше нравится?

Как найти корень числа в Excel? Функция Корень

Как мы знаем, что квадратный корень числа — это число в степени 0,5 (1/2). Поэтому найти корень числа также просто как и возвести в любую степень. Если хотите извлечь из четырех корень из 2, то запишите =СТЕПЕНЬ(4;0,5). Или для этого есть специальная функция =КОРЕНЬ(Число). Показываю сразу несколько способов извлечь корень числа.

Как красиво записать степень в Excel в подписи к расчетам?

Сейчас поговорим, как красиво записать подписи к формулам. Под красивой записью мы подразумеваем т.н. надстрочный шрифт. Как здесь:

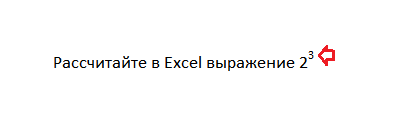
Так сделать очень просто, выделите в строке формул или в ячейке число, обозначающее степень (то что надо сделать маленьким).

Табличный процессор Microsoft Excel позволяет выполнять с данными самые разные операции. Но, если простые операции, вроде сложения, у пользователей не вызывают трудностей. То, с более сложными, например, с возведением в степень, бывают проблемы.

В этом материале мы расскажем о том, как возвести в степень в Excel. Статья будет актуальна для всех версий табличного процессора Excel, включая Excel 2003, 2007, 2010, 2013 и 2016.

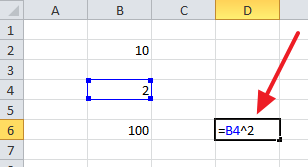
Самый простой способ возвести число или ячейку в степень в Экселе, это воспользоваться символом «^», который находится на клавише 6 на клавиатуре и вводится с помощью комбинации клавиш Shift-6 в английской раскладке клавиатуры.

Для того чтобы воспользоваться данным способом возведения в степень просто установите курсор в нужную вам ячейку и введите формулу «=B2^B4». Где B2 – это адрес ячейки с числом, которое вы хотите возвести в степень, а B4 – адрес ячейки со степенью.

После ввода формулы нажмите на клавишу Enter и в выбранной вами ячейки таблицы вы получите результат возведения в степень.

Данный прием работает не только с адресами ячеек, но и с обычными числами. Вводим в любую ячейку таблицы Эксель «=10^2»

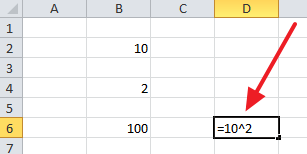
Также в рамках формулы можно одновременно использовать, как адреса ячеек, так и обычные числа.

С этим читают

Местонахождение

Добавить функцию на рабочий лист можно несколькими способами:

1. Через вкладку Формулы на Панели инструментов. Из библиотеки выбираете Математические и ищете КОРЕНЬ.

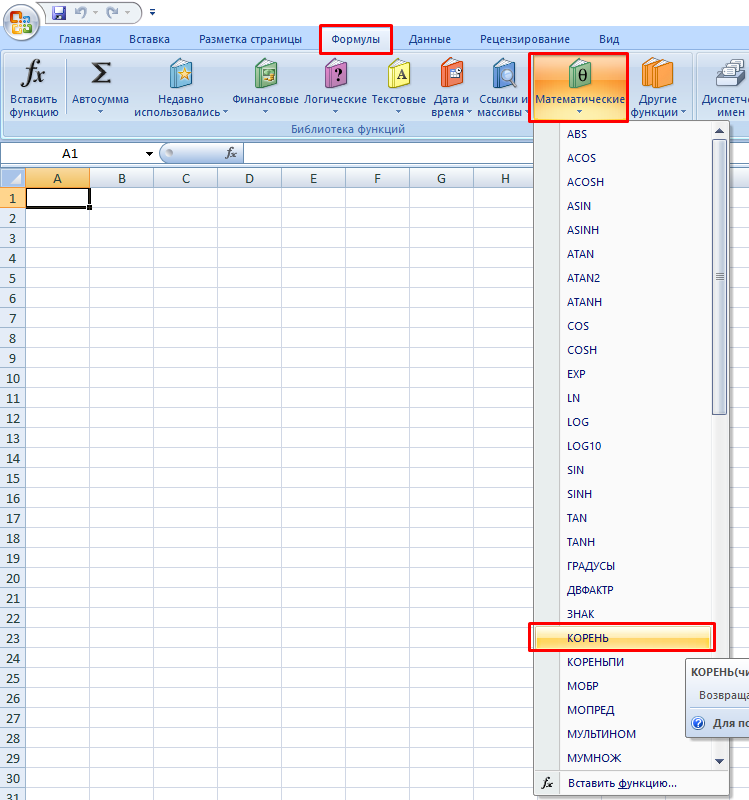
На заметку! Если Вы используете не русскоязычную версию редактора, то на английском данная функция пишется как sqrt. Такая аббревиатура используется во многих языках программирования.

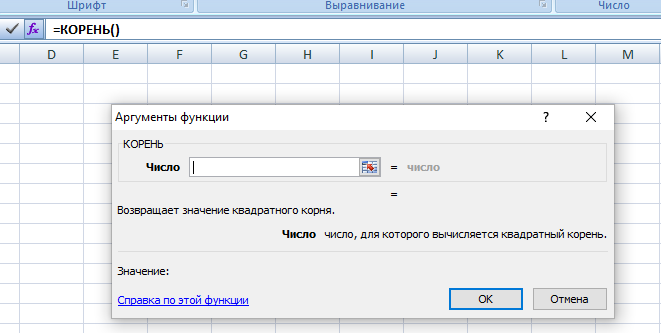
1. Используя специальный мастер. Сначала вызываете окно выбора формулы, затем добавляете значение аргумента.

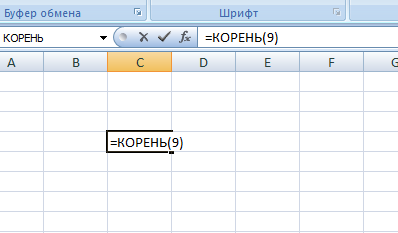
1. Вписываете напрямую в ячейку. Не забывайте вначале записи поставить знак равно, чтобы редактор распознал начало формулы.

https://youtube.com/watch?v=j08cHYw2x4Q

Способы извлечения

Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.

Способ 1: применение функции

Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:

Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.

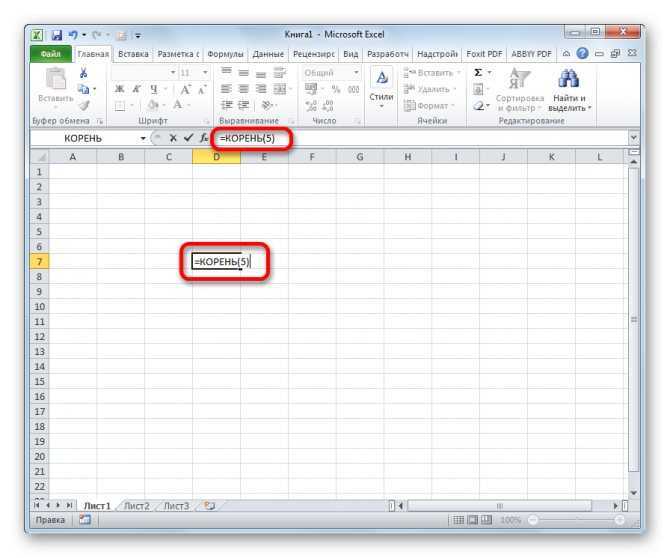
Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.

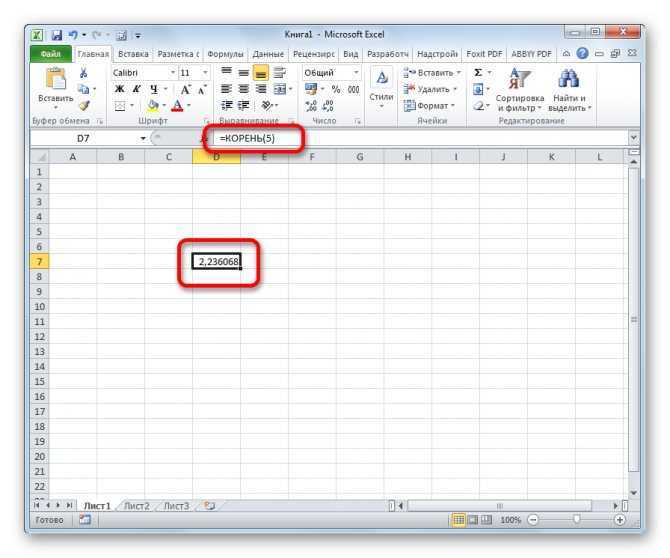
Кроме того, можно применить данную формулу через мастер функций.

1. Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.

Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена. Достаточно кликнуть по этой ячейке, чтобы её адрес был внесен в поле. После ввода данных жмем на кнопку «OK».

1. Выделяем ячейку для отображения результата расчета. Переходим во вкладку «Формулы».

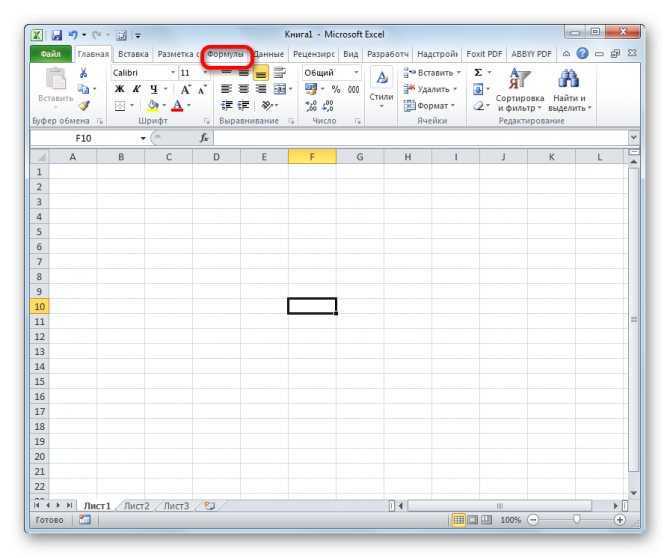
В блоке инструментов «Библиотека функций» на ленте кликаем по кнопке «Математические». В появившемся списке выбираем значение «КОРЕНЬ».

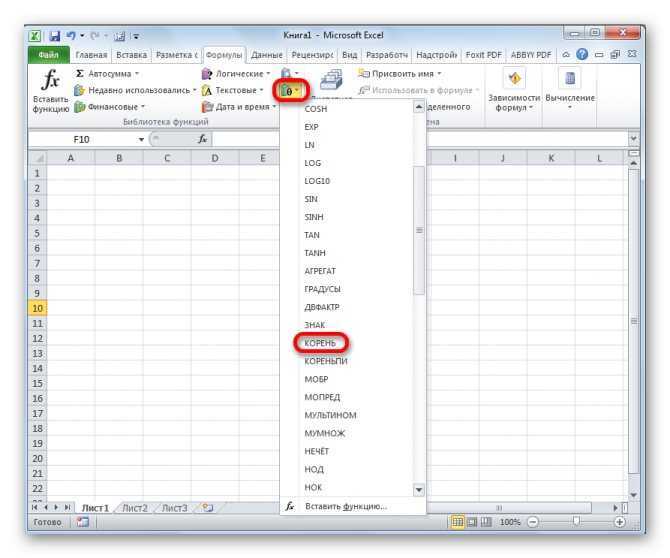
Открывается окно аргументов. Все дальнейшие действия в точности такие же, как и при действии через кнопку «Вставить функцию».

Способ 2: возведение в степень

Рассчитать кубический корень использование указанного выше варианта не поможет. В этом случае величину нужно возвести в дробную степень. Общий вид формулы для расчета таков:

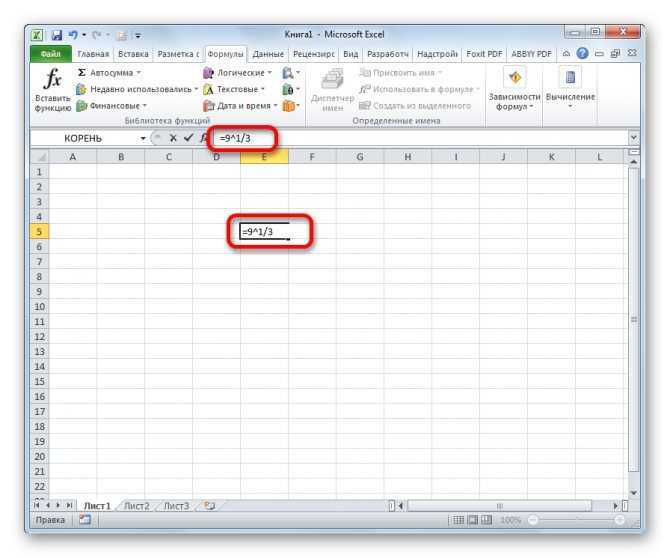
То есть, формально это даже не извлечение, а возведение величины в степень 1/3. Но данная степень и является корнем кубическим, поэтому именно такое действие в Эксель используется для его получения. В эту формулу вместо конкретного числа также можно вписать координаты ячейки с числовыми данными. Запись производится в любой области листа или в строке формул.

Извлечение корня в Excel с помощью формулы и функции

Среди базовых математических вычислений помимо сложения, вычитания, умножения и деления можно выделить возведение в степень и обратное действие – извлечение корня. Давайте посмотрим, каким образом можно выполнить последнее действие в Эксель разными способами.

• Метод 1: использование функции КОРЕНЬ
• Метод 2: нахождение корня путем возведения в степень
• Заключение

Метод 1: использование функции КОРЕНЬ

Множество операций в программе реализуется с помощью специальных функций, и извлечение корня – не исключение. В данном случае нам нужен оператор КОРЕНЬ, формула которого выглядит так:

=КОРЕНЬ(число)

Для выполнения расчета достаточно написать данную формулу в любой свободной ячейке (или в строке формул, предварительно выбрав нужную ячейку). Слово “число”, соответственно, меняем на числовое значение, корень которого нужно найти.

Когда все готово, щелкаем клавишу Enter и получаем требуемый результат.

Вместо числа можно, также, указать адрес ячейки, содержащей число.

Указать координаты ячейки можно как вручную, прописав их с помощью клавиш на клавиатуре, так и просто щелкнув по ней, когда курсор находится в положенном месте в формуле.

Вставка формулы через Мастер функций

Воспользоваться формулой для извлечения корня можно через окно вставки функций. Вот, как это делается:

1. Выбрав ячейку, в которой мы хотим выполнить расчеты, щелкаем по кнопке “Вставить функцию” (fx).
2. В окне мастера функций выбираем категорию “Математические”, отмечаем оператор “КОРЕНЬ” и щелкаем OK.
3. Перед нами появится окно с аргументом функции для заполнения. Как и при ручном написании формулы можно указать конкретное число или ссылку на ячейку, содержащую числовое значение. При этом, координаты можно указать, напечатав их с помощью клавиатуры или просто кликнуть по нужному элементу в самой таблице.

Вставка функции через вкладку “Формулы

1. Встаем в ячейку, в которой хотим произвести вычисления. Щелкаем по кнопке “Математические” в разделе инструментов “Библиотека функций”.
2. Пролистав предложенный перечень находим и кликаем по пункту “КОРЕНЬ”.
3. На экране отобразится уже знакомое окно с аргументом, который нужно заполнить, после чего нажать кнопку OK.

Метод 2: нахождение корня путем возведения в степень

Описанный выше метод позволяет с легкостью извлекать квадратный корень из числа, однако, для кубического уже не подходит. Но и эта задача в Excel реализуема. Для этого числовое значение нужно возвести в дробную степень, где в числителе будет стоять “1”, а в знаменателе – цифра, означающая степень корня (n).

В общем виде, формула выглядит так:

=(Число)^(1/n)

Безусловным преимуществом такого способа является то, что мы можем извлечь корень любой степени, заменив букву “n” в знаменателе дроби на требуемую цифру.

Для начала давайте рассмотрим формулу для извлечения квадратного корня. Она выглядит следующим образом: =(Число)^(1/2).

Соответственно, для расчета кубического корня будет использоваться выражение ниже:

=(Число)^(1/3)

Допустим, нам нужно извлечь кубический корень из числа 27. В этом случае нужно записать в ячейке такую формулу: =27^(1/3).

Нажав Enter, получаем результат вычислений.

Аналогично работе с функцией КОРЕНЬ, вместо конкретного числа можно указать ссылку на ячейку.

Заключение

Таким образом, в Excel можно без особых усилий извлечь корень из любого числа, и сделать это можно разными способами. К тому же, возможности программы позволяют выполнять расчеты для извлечения не только квадратного, но и кубического корня. В редких случаях требуется найти корень n-степени, но и эта задача достаточно просто выполняется в программе.

Способ 3: написание степени в ячейке таблицы

Если вы хотите непосредственно в ячейке указать степень числа, тогда необходимо использовать надстрочный знак. На самом деле выполнение такой записи не является чрезвычайно сложным, просто алгоритм действия для этого не совсем понятен рядовому пользователю, ведь перед самой записью потребуется сделать еще некоторое приготовление. Но обо всем по порядку. Давайте рассмотрим все на примере, чтобы сразу было понятно, как это работает. Разбирать будем все тот же случай, когда нам требуется возвести число 3 в четвертую степень.

1. Выделите ячейку, в которой хотите сделать запись.
2. Измените ее формат на текстовый. Для этого, находясь на главной вкладке, на панели инструментов нажмите по выпадающему списку, расположенному в группе «Число». В появившемся списке выберите пункт «Текстовый».
3. Теперь все готово для того, чтобы запись в ячейке отобразилась корректно. Итак, введите в нее число 34. Почему именно его? Да потому, что 4 – это степень числа 3, которую мы сейчас будем видоизменять.
4. Выделите в ячейке непосредственно саму цифру 4.
5. Нажмите на клавиатуре горячие клавиши Ctrl+1.
6. Появится окно «Формат ячеек». В нем вам необходимо в области «Видоизменение» установить отметку напротив пункта «Надстрочный».
7. Нажмите ОК.